CBCTF躲猫猫题解 [ Sorry yolbby ]

前言

拖了好久好久的题解，出完题整个人都会变得懒得复盘，可能出的时候都是一整个稀里糊涂的状态，想着怎么做到尽可能知识点简单&有趣&能做出筛选，但最终结果好像不是很尽如人意，四道题第一天就上了到最后也没什么人在看，算是整了盘大的。招新赛那天正在跨年，当时早上去老婆大人买了三大袋零食，下午一边双扣一边运维，看着其他方向的题矻矻被出，密码题无人问津，脑子都坏掉了。带着队友去吃了顿鸡啤咯哒以消解愁绪，也算过了个难忘的新年吧。

Anyway话不多说，就让厨师把一整道菜都端上来瞧瞧吧。

躲猫猫1

跨年夜当然少不了团建活动！

冬天雪花飘飘正适合玩躲猫猫，为配合赛博主题，0RAYS的每个队员身上都带着一小段flag，拼起来就可以兑换过年大礼包！你毛遂自荐作为抓捕者，于是队员们悄眯眯地藏起来了。

夜晚静悄悄的，你数完数踏出起点，影影绰绰看到几个人影......

import random
from Crypto.Util.number import *
from secret import flag

humble_part, Ech0_part, Z3r0_part = flag[:len(flag)//3],flag[len(flag)//3:2*len(flag)//3],flag[2*len(flag)//3:]

#学活广场 humb1e似乎在旗杆背后探头探脑
secret = bin(bytes_to_long(humble_part))[2:]
R.<humb1e> = PolynomialRing(GF(getPrime(50)))
R = R.quo(humb1e^30+random.randint(1,2^49)*humb1e+1)
look_for_humb1e = [R(humb1e ^ (1500*random.choice([ord('h'),ord('u'),ord('m'),ord('b'),ord('1'),ord('e')]))) if i == '1' else R.random_element() for i in secret]

#都放假了四教还亮着灯？抓到Ech0在躲猫猫的时候偷学密码！
secret = bin(bytes_to_long(Ech0_part))[2:]
look_for_Ech0 = [prod([j[0]^(j[1]-1)*(j[0]-1) for j in factor(random.getrandbits(100))]) if i == '1' else getPrime(100)-1 for i in secret]

#雪下得好大，花圃周围的亮白色身影是Z3r0吗
secret = bin(bytes_to_long(Z3r0_part))[2:]
p = getPrime(512)
look_for_Z3r0 = [pow(31137,65537,p*getPrime(512)) if i == '1' else pow(31137,65537,getPrime(512)*getPrime(512)) for i in secret]

print(look_for_humb1e)
print(look_for_Ech0)
print(look_for_Z3r0)

humb1e's part

#学活广场 humb1e似乎在旗杆背后探头探脑
secret = bin(bytes_to_long(humble_part))[2:]
R.<humb1e> = PolynomialRing(GF(getPrime(50)))
R = R.quo(humb1e^30+random.randint(1,2^49)*humb1e+1)
look_for_humb1e = [R(humb1e ^ (1500*random.choice([ord('h'),ord('u'),ord('m'),ord('b'),ord('1'),ord('e')]))) if i == '1' else R.random_element() for i in secret]

Roll了一个多项式商环R，然后去在环上进行运算。令R函数表示随机，那么此时我们对于flag的不同位数，有 \[ \begin{gather} flag[i]=1:humb1e^{1500*R(h,u,m,b,1,e)} \\ flag[i]=0:Random \space element \ \end{gather} \] 那么显然，在数据当中出现次数大于1次极有可能等价于flag[i]=1（因为modulus的度有30），统计一下就可以恢复flag串。

from Crypto.Util.number import *

R.<humb1ebar> = PolynomialRing(ZZ)
data = 

flag = ''.join('1' if data.count(data[i]) > 1 else '0' for i in range(len(data)))
print(long_to_bytes(int(flag,2)))
#CBCTF{H4ppy_N3wyear

Ech0's part

1
2
3

#都放假了四教还亮着灯？抓到Ech0在躲猫猫的时候偷学密码！
secret = bin(bytes_to_long(Ech0_part))[2:]
look_for_Ech0 = [prod([j[0]^(j[1]-1)*(j[0]-1) for j in factor(random.getrandbits(100))]) if i == '1' else getPrime(100)-1 for i in secret]

这个部分的处理更加清晰，即随机roll一个数、并计算它的欧拉函数，有 \[ \begin{gather} flag[i]=1:Φ(Random \space number) \\ flag[i]=0:Φ(Prime \space number) \end{gather} \] 那么这个时候我们需要进行两层判断，第一层是判断所给数值加上一是否为素数，第二层是判断素数的bit数是否为100。代码如下

from Crypto.Util.number import *

data = 

flag = ''.join('0' if is_prime(data[i]+1) and len(bin(data[i]+1)[2:]) == 100 else '1' for i in range(len(data)))
print(long_to_bytes(int(flag,2)))
#!Hope_y0u^can_h4ve_

此时不排除随机数就是bit数为100的素数，因此可以debug得出正确的flag

1	#!Hope_y0u_can_h4ve_

Z3r0's part

#雪下得好大，花圃周围的亮白色身影是Z3r0吗
secret = bin(bytes_to_long(Z3r0_part))[2:]
p = getPrime(512)
look_for_Z3r0 = [pow(31137,65537,p*getPrime(512)) if i == '1' else pow(31137,65537,getPrime(512)*getPrime(512)) for i in secret]

对于flag二进制位上的数字，令Q为随机素数，有 \[ \begin{gather} flag[i]=1:31337^{65537} \enspace mod \enspace p·Q\\ flag[i]=0:31337^{65537} \enspace mod \enspace Q_1·Q_2\\ \end{gather} \] 两个flag位等于1的数据\(c_1,c_2\)有关系如下 \[ \begin{gather} c_1=31337^{65537}+k_1pQ_1\\ c_2=31337^{65537}+k_2pQ_2\\ \end{gather} \] 因此可以得到关系 \[ c_1-c_2=(k_1Q_1-k_2Q_2)p \] 然后玩法就多了，可以考虑用gcd把p求出来然后求证每个数据在\(GF(p)\)上是否与\(31337^{65537}\)等价，这样在求出p以后每个数据都只使用一次，就能够完成最后flag的求解。

from Crypto.Util.number import *

data = 

for i in range(1,len(data)):
    for j in range(i+1,len(data)):
        if gcd(data[0]-data[i],data[0]-data[j]) > 2^200:
            p = gcd(data[0]-data[i],data[0]-data[j])
            break
            
assert is_prime(p)

flag = ''.join('1' if data[i]%p == pow(31137,65537,p) else '0' for i in range(len(data)))
print(long_to_bytes(int(flag,2)))
#fun_1n_CBCTF_Juni0r}

躲猫猫2

Humb1e，Ech0，Z3r0藏得都太草率了，显然没有把游戏放在心上。你语重心长地批评了他们一顿，踏上寻找其他人的旅途。

这下游戏就没有那么简单了。已经拿到一个新年大礼包的你能否再次创造奇迹呢？

import random
from Crypto.Util.number import *
from Crypto.Cipher import AES
import os
from secret import flag

gtg_part, beeee_part, Seg_Tree_part = flag[:len(flag)//3],flag[len(flag)//3:2*len(flag)//3],flag[2*len(flag)//3:]


#你惊异地发现，树丛里黑糊糊的枝叶居然有点神似gtg的辫子
secret = bin(bytes_to_long(gtg_part))[2:]

def matrix_crt(mp,mq,p,q):
    m = matrix(Zmod(p*q),[[crt([int(mp[i,j]),int(mq[i,j])],[p,q]) for i in range(2)] for j in range(2)])
    return m

p = getPrime(20)
a,b = MatrixGroup(matrix(GF(149),[[41,21],[82,81]])),MatrixGroup(matrix(GF(163),[[41,21],[82,81]]))
ma,mb = a.gens()[0],b.gens()[0]

look_for_gtg = [list(matrix_crt(matrix(ZZ,ma^random.randint(1,p)),matrix(ZZ,mb^random.randint(1,p)),149,163)) if i == '1' else list(matrix(Zmod(149*163),[[random.randint(1,149*163)for _ in range(2)] for __ in range(2)])) for i in secret]


#前两天刚考完研，图书馆难得清静，你在9楼搜寻，只见角落闪烁着微光。好像是beeee！
secret = bin(bytes_to_long(beeee_part))[2:]
m,p = getPrime(1023),getPrime(1024)

def ppallier(m,p):
    c = pow(p+1,getPrime(40)*m,p^2)*pow(random.randint(1,p^2-1),p,p^2)%p^2
    return c

look_for_beeee = [pow(ppallier(m,p),p-1,p^2) if i == '1' else random.randint(1,p^2-1) for i in secret]


#看上去有人卡视野藏在协会天台上。你走了过去，Seg_Tree正在假装自己是一颗树。
secret = bin(bytes_to_long(Seg_Tree_part))[2:]
look_for_Seg_Tree = [AES.new(key = os.urandom(16),mode = AES.MODE_CFB,iv = os.urandom(16)).decrypt((os.urandom(16)*3)[:33]) if i == '1' else AES.new(key = os.urandom(16),mode = AES.MODE_CFB,iv = os.urandom(16)).encrypt((os.urandom(16)*3)[:33]) for i in secret]


print(look_for_gtg)
print(look_for_beeee)
print(look_for_Seg_Tree)

gtg's part

#你惊异地发现，树丛里黑糊糊的枝叶居然有点神似gtg的辫子
secret = bin(bytes_to_long(gtg_part))[2:]

def matrix_crt(mp,mq,p,q):
    m = matrix(Zmod(p*q),[[crt([int(mp[i,j]),int(mq[i,j])],[p,q]) for i in range(2)] for j in range(2)])
    return m

p = getPrime(20)
a,b = MatrixGroup(matrix(GF(149),[[41,21],[82,81]])),MatrixGroup(matrix(GF(163),[[41,21],[82,81]]))
ma,mb = a.gens()[0],b.gens()[0]

look_for_gtg = [list(matrix_crt(matrix(ZZ,ma^random.randint(1,p)),matrix(ZZ,mb^random.randint(1,p)),149,163)) if i == '1' else list(matrix(Zmod(149*163),[[random.randint(1,149*163)for _ in range(2)] for __ in range(2)])) for i in secret]

定义了两个矩阵群，并令两个矩阵群的生成元数值相同，群a位于\(GF(149)\)，群b位于\(GF(163)\)，数据与flag位的关系如下 \[ \begin{gather} flag[i]=1:M=CRT([m^{r_a},m^{r_b}],[149,163])\\ flag[i]=0:M=RandomMatrix \end{gather} \] 我们把CRT过程分成两半来进行考虑，\(M\)矩阵模\(149\)时得到矩阵\(m^{r_a}\)，同理模\(163\)时得到矩阵\(m^{r_b}\)，那么令\(m\)在a中的阶为\(oa\)，令\(m\)在\(b\)中的阶为\(ob\)，对于flag为1的数，把它们放在模p下进行以oa为幂的幂运算，放在模q下进行以ob为幂的幂运算，可以得到下列式子 \[ \begin{gather} M^{oa}=m^{ra*oa}=E~mod~p\\ M^{ob}=m^{rb*ob}=E~mod~q \end{gather} \] 因此在两边都会得到单位矩阵，通过这个性质我们可以区分所有的数据。

from Crypto.Util.number import *
a,b = MatrixGroup(matrix(GF(149),[[41,21],[82,81]])),MatrixGroup(matrix(GF(163),[[41,21],[82,81]]))

oa,ob = a.order(),b.order()
data = 

flag = ''.join('1' if matrix(GF(149),data[i])^(oa) == identity_matrix(2) and matrix(GF(163),data[i])^(ob) == identity_matrix(2) else '0' for i in range(len(data)))
print(long_to_bytes(int(flag,2)))
#b'CBCTF{W1sh_Y\xb0ur_N3xt_Y3'

同样是debug一下，还原出flag

1	b'CBCTF{W1sh_Y0ur_N3xt_Y3'

beeee's part

#前两天刚考完研，图书馆难得清静，你在9楼搜寻，只见角落闪烁着微光。好像是beeee！
secret = bin(bytes_to_long(beeee_part))[2:]
m,p = getPrime(1023),getPrime(1024)

def ppallier(m,p):
    c = pow(p+1,getPrime(40)*m,p^2)*pow(random.randint(1,p^2-1),p,p^2)%p^2
    return c

look_for_beeee = [pow(ppallier(m,p),p-1,p^2) if i == '1' else random.randint(1,p^2-1) for i in secret]

基于pallier，把pallier里的若干参数都替换成了p，底数也从pq替换成为p^2，加密消息不变。 \[ \begin{gather} flag[i]=1:ppallier(m,p)\\ flag[i]=0:RandomNumber \end{gather} \] 首先对于ppallier加密的数据，有 \[ c=(p+1)^{km}r^p~mod~p^2\\ \] 根据二项式定理， \[ (p+1)^{km}=1+kmp~mod~p^2 \] 而后半部分的随机数相关部分可以通过\(p-1\)的幂运算消除，类似Z3r0，进行相似的分析， \[ \begin{gather} c_1^{p-1}=1+k_1mp(p-1)=1-pk_1m~mod~p^2\\ c_2^{p-1}=1+k_2mp(p-1)=1-pk_2m~mod~p^2 \end{gather} \] 因此这里其实就又只是一个gcd，不同点在于这里要筛出一个为1的点，拿三个点进行多次比较，如果gcd值够大就记为1。啊哈哈，真是炒冷饭大师啊。

from Crypto.Util.number import *
data = 

def get1_i(data):
    for i in range(1,len(data)):
        for j in range(i+1,len(data)):
            if gcd(data[0]-data[i],data[0]-data[j]) > 2^200:
                return i

i1 = get1_i(data)
flag = ''.join('1' if i in [i1,0] or gcd(data[i1]-data[i],data[0]-data[i]) > 2^200 else '0' for i in range(len(data)))
print(long_to_bytes(int(flag,2)))
#ar_fulf111ed_w1th_h4pp1

Seg_Tree's part

1
2
3

#看上去有人卡视野藏在协会天台上。你走了过去，Seg_Tree正在假装自己是一颗树。
secret = bin(bytes_to_long(Seg_Tree_part))[2:]
look_for_Seg_Tree = [AES.new(key = os.urandom(16),mode = AES.MODE_CFB,iv = os.urandom(16)).decrypt((os.urandom(16)*3)[:33]) if i == '1' else AES.new(key = os.urandom(16),mode = AES.MODE_CFB,iv = os.urandom(16)).encrypt((os.urandom(16)*3)[:33]) for i in secret]

考的是CFB模式里有个特性，即移位寄存器使用密文填充。

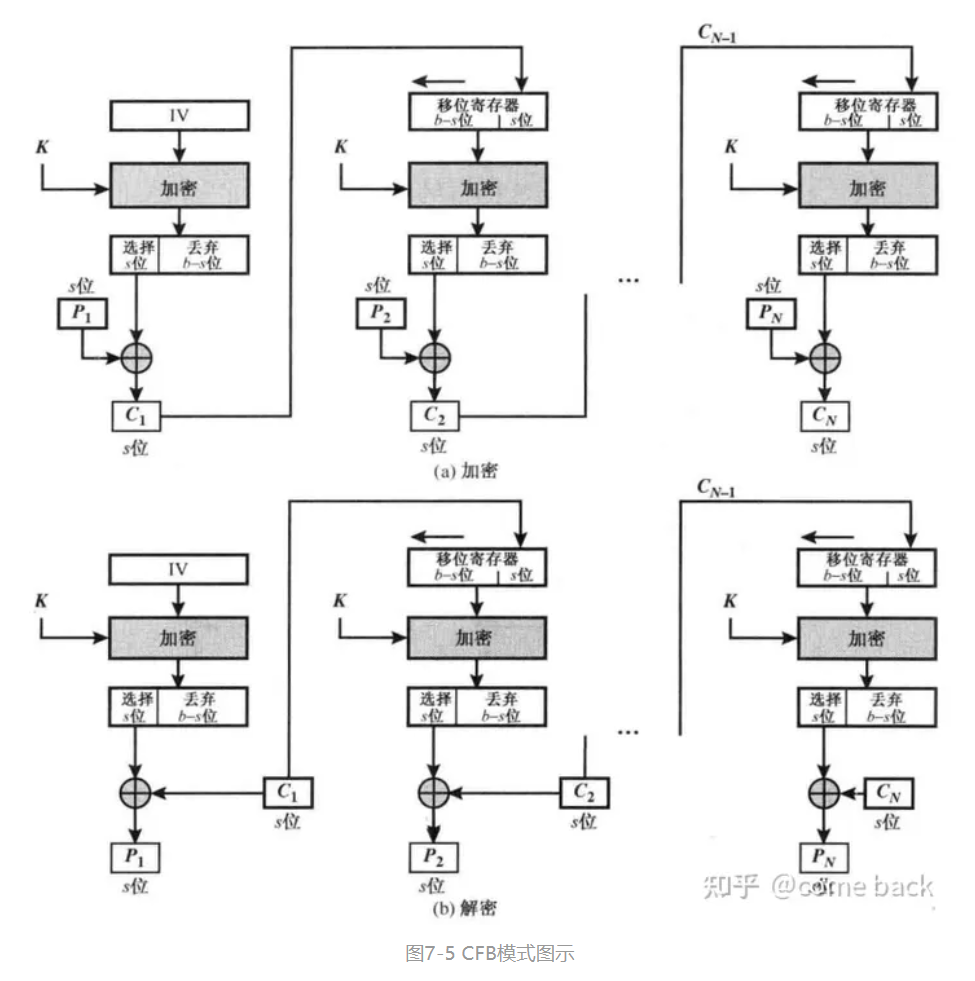
由于移位寄存器中填充的是密文，因此当密文以16byte为单位进行重复时，移位寄存器中每隔16byte也会出现一次重复，因此如果结果中的第17个byte和第33个byte相同，则说明使用的是decrypt。题目中特意卡了一个33，目的也是在于做出提示。

from Crypto.Util.number import *

data = 

flag = ''.join('1' if data[i][16] == data[i][-1] else '0' for i in range(len(data)))
print(long_to_bytes(int(flag,2)))
#b'ness_4nd_s4t1sfic4t10n!}'

躲猫猫3

你花了点力气找到了gtg，beeee和Seg_Tree。手握两份新年礼包的你显然已经是整个协会中最富有的哥们儿，你一边畅想着未来的幸福生活和完美外设一边哼哧瘪肚在冬日里前行。

剩下的人都是难找的茬子啊......

不过你坚信这一切难不倒你。

import random
from Crypto.Util.number import *
from Crypto.Cipher import AES
import os
from secret import flag

Art0ne_part, 奶茶_part, _1manity_part = flag[:len(flag)//3],flag[len(flag)//3:2*len(flag)//3],flag[2*len(flag)//3:]

#Art0ne偷溜进体育馆，在走廊的一个拐角随时准备逃跑。你抓住他时自己已经要累得不行了。
secret = bin(bytes_to_long(Art0ne_part))[2:]

from secret import p,q
n = 7589728368000360290382663172234488251897043335410016881502715294598442607646158403453736522549655542481555536223060519309001243744487805230719883633463721
assert n == p * q and isPrime(p) and isPrime(q) and len(bin(p)) == 258 and len(bin(q)) == 258

R.<x> = PolynomialRing(Zmod(n))

def roll(mode,i):
    if mode == 0:
        return random.randint(1,p*q-1)
    else:
        x,y = random.randint(1,2^80),random.randint(1,2^256)*p
        return R(x+x*y^2+y*x^3)
    
look_for_Art0ne = [roll(1,i) if secret[i] == '1' else roll(0,i) for i in range(len(secret))]


#你找遍了学校，最后在弗雷德二店的古茗二楼意外找到了奶茶并宣判他犯规
secret = bytes_to_long(奶茶_part)

def shuffle(ll,lr):
    a = ['0']*len(奶茶_part)*ll+['1']*len(奶茶_part)*lr
    random.shuffle(a)
    return a

look_for_奶茶 = [int(''.join(shuffle(5,3)),2)^^secret if i == '1' else int(''.join(shuffle(3,5)),2)^^secret for i in bin(secret)[2:].rjust(8*len(奶茶_part),'0')]


#1manity藏在师生驿站，跨年夜店里没有值班，乌漆嘛黑的还带个笨蛋智能门锁，要不是你渴了进去买杯饮料还真的找不到他
secret = bin(bytes_to_long(_1manity_part))[2:]

p = 13692367685268431611
x = [matrix(GF(p),4,4,[random.randint(1,p-1) for i in range(16)]) for i in range(7)]

look_for_1manity = [list(sum(random.randint(1,p-1)*j for j in x)) if i == '1' else list(matrix(GF(p),4,4,[random.randint(1,p-1) for i in range(16)])) for i in secret]


print(look_for_Art0ne)
print(look_for_奶茶)
print(look_for_1manity)

Art0ne's part

from secret import p,q
n = 7589728368000360290382663172234488251897043335410016881502715294598442607646158403453736522549655542481555536223060519309001243744487805230719883633463721
assert n == p * q and isPrime(p) and isPrime(q) and len(bin(p)) == 258 and len(bin(q)) == 258

R.<x> = PolynomialRing(Zmod(n))

def roll(mode,i):
    if mode == 0:
        return random.randint(1,p*q-1)
    else:
        x,y = random.randint(1,2^80),random.randint(1,2^256)*p
        return R(x+x*y^2+y*x^3)
    
look_for_Art0ne = [roll(1,i) if secret[i] == '1' else roll(0,i) for i in range(len(secret))]

经典copper，一个类似已知p高位的情况，给出的条件可以简化成\(kp+p_h\)的形式，所以直接拿比较宽松的参数去打就行。

from Crypto.Util.number import *

n = 
data = 
R.<x> = PolynomialRing(Zmod(n))

flag = ''.join('1' if (data[i]-x).monic().small_roots(beta = 0.45,x = 2^80,epsilon = 0.02) else '0' for i in range(len(data)))
print(long_to_bytes(int(flag,2)))
#CBCTF{4nd_we_W1sh_y0u_Br1mm3

奶茶's part

#你找遍了学校，最后在弗雷德二店的古茗二楼意外找到了奶茶并宣判他犯规
secret = bytes_to_long(奶茶_part)

def shuffle(ll,lr):
    a = ['0']*len(奶茶_part)*ll+['1']*len(奶茶_part)*lr
    random.shuffle(a)
    return a

look_for_奶茶 = [int(''.join(shuffle(5,3)),2)^^secret if i == '1' else int(''.join(shuffle(3,5)),2)^^secret for i in bin(secret)[2:].rjust(8*len(奶茶_part),'0')]

相当于每个flag的位数都和最终的数据有两重关系，第一重关系在于当前flag的位数会影响异或运算的结果；第二重关系在于当前flag的位数会影响异或bit串的生成。当当前位置bit数为1时，01比为5:3；当前位置bit数为0时，01比为3:5。

而我们已知第一个bit一定是0，可以利用的点在于，两个bit数相同的位置生成的异或bit串重合度从概率上来说显著高于两个bit数不同的位置生成的异或bit串重合度。那么我们可以设计一种算法对这种性质加以利用：

将与第一个bit所生成的bit串重合度最低的若干个bit串所在序号暂时标记为'1'
我们有'1'中多0少1的性质，由于'1'集合中'0'占比较大，说明各个bit中与0异或的可能性较大，因此我们统计当前'1'集合中各个bit的出现1的概率，出现1概率较大，说明当前位置很可能是'1'，反之就说明当前位置很可能是'0'。这样，我们就可以更新得到一个更大的'0'集合和'1'集合。
对于'0'集合，将它的所有位与1异或，转变成一个符合'1'集合的特征的数据，不断缩小阈值、扩大集合，最终恢复所有位数。

小插曲：居然发现了测题的时候留下的代码，这样就省去了重写的功夫，不过看起来有些冗余，就勉强勉强。其中a变量填上题目给的数据。

a = 

def dif(a,b):
    n = 0
    for i,j in zip(a,b):
        if i!=j:
            n += 1
    return n

c = []
for i in a:
    c.append(bin(i)[2:].rjust(len(a),'0'))

d = []
for i in range(len(a)-1):
    if (dif(c[0],c[i+1])) > len(a)//2:
        d.append(c[i+1])

mtxt = ''
for i in [sum([int(i[j]) for i in d]) for j in range(len(a))]:
    if i >= len(d)*4//7:
        mtxt += '1'
    elif i <= len(d)*3//7:
        mtxt += '0'
    else:
        mtxt += '2'

for _ in range(4):
    d = []
    for i in range(len(a)):
        if mtxt[i] == '1':
            d.append(c[i])
        elif mtxt[i] == '0':
            d.append(''.join(str(1-int(j)) for j in c[i]))
    m = [sum([int(i[j]) for i in d]) for j in range(len(a))]
    mtxt = ''
    for i in m:
        if i/len(d) >= 0.6-0.03*_:
            mtxt += '1'
        elif i/len(d) <= 0.4+0.03*_:
            mtxt += '0'
        else:
            mtxt += '2'

print(mtxt)
print(long_to_bytes(int(mtxt,2)))
#d_ov3r_with_wisd0m_&_g3t_int

1manity's part

#1manity藏在师生驿站，跨年夜店里没有值班，乌漆嘛黑的还带个笨蛋智能门锁，要不是你渴了进去买杯饮料还真的找不到他
secret = bin(bytes_to_long(_1manity_part))[2:]

p = 13692367685268431611
x = [matrix(GF(p),4,4,[random.randint(1,p-1) for i in range(16)]) for i in range(7)]

look_for_1manity = [list(sum(random.randint(1,p-1)*j for j in x)) if i == '1' else list(matrix(GF(p),4,4,[random.randint(1,p-1) for i in range(16)])) for i in secret]

给了若干个4×4矩阵，我们需要从中找出由七个未知矩阵进行线性运算构成的矩阵。题目当中我们已知尾byte为'}'=0b1111101、首bit为'1'，因此手上正好7个已知1bit。

我们把矩阵看作长度为16的向量，那么就能够知道，只要它们线性无关，由于剩下的向量与这些向量都由同样的基构成，因此将7个已知向量与一个验证向量拼成的8×16的矩阵的秩仍然是7；反之，如果秩为8，说明验证向量是随机生成的。

from Crypto.Util.number import *
def m2v(a):
    return vector(ZZ,16,list(a[0])+list(a[1])+list(a[2])+list(a[3]))

p = 13692367685268431611
data = 
data = [m2v(i) for i in data]
m = [data[0],data[-7],data[-6],data[-5],data[-4],data[-3],data[-1]]

flag = ''.join('1' if matrix(GF(p),m + [i]).rank() == 7 else '0' for i in data)
print(long_to_bytes(int(flag,2)))
#b'3rest3d_in_fi3ld_you_w0rk_0n}'

躲猫猫4

说来奇怪，在1manity，Art0ne和奶茶之后，你找遍了一整个学校都没能找到剩下的人，只能启动planB，使用你长期修炼凝结而成的密码解析技巧去把他们的参数调出来一一分析。

你以为你稳操胜券，但定睛一看，JBNRZ居然开了外挂卡在墙的里面！

他也把misc技巧带出了虚拟世界！

这个发现震惊了你的世界观，随着你打开每个人的视角偷看他们的位置，你的下巴不知不觉掉到了地上。

import random
from Crypto.Util.number import *
from Crypto.Cipher import AES
import os
from secret import flag

JBNRZ_part, pankas_part, v0id_part = flag[:len(flag)//3],flag[len(flag)//3:2*len(flag)//3],flag[2*len(flag)//3:]

#JBNRZ开了修改器把自己卡在七教二楼阳台的墙壁中间。你就算知道他在哪，也没法摸到他。
secret = bin(bytes_to_long(JBNRZ_part))[2:]

q = 0x1a0111ea397fe69a4b1ba7b6434bacd764774b84f38512bf6730d2a0f6b0f6241eabfffeb153ffffb9feffffffffaaab
r = 0x73eda753299d7d483339d80809a1d80553bda402fffe5bfeffffffff00000001
k = GF(r)(q).multiplicative_order()
F = GF(q)
K2.<x> = PolynomialRing(F)
F2.<u> = F.extension(x^12+1)
E2 = EllipticCurve(F2, [0, 4+4*u])
o = E2.order()

P = E2.random_element()*(o//r)
Q = E2.random_element()*(o//r)
R = E2.random_element()*(o//r)
S = E2.random_element()*(o//r)

def random_gen_fg(P,Q,R,S):
    P,Q,R,S = random.randint(1,r-1)*P,random.randint(1,r-1)*Q,random.randint(1,r-1)*R,random.randint(1,r-1)*S
    f1 = (P._miller_(Q+S,r))
    f2 = (P._miller_(S,r))
    g1 = (Q._miller_(P+R,r))
    g2 = (Q._miller_(R,r))
    return P.weil_pairing(Q,r)+(f1/f2*g2/g1)

look_for_JBNRZ = [random_gen_fg(P,Q,R,S) if i == '1' else random.randint(1,q-1)*u+random.randint(1,q-1) for i in secret]


#pankas用注释符把自己注释掉了，你必须使用一些过滤手段停止他的作弊行为。
secret = bytes_to_long(pankas_part)

p = 567811
F = GF(p)
n, k, r= 16, 10, 6
t = n//4

C = codes.GeneralizedReedSolomonCode([F(_+1) for _ in range(n)],k)
S = matrix(F,r,r,[(155790, 486108, 98452, 364639, 120720, 313488), (100323, 367952, 158314, 537951, 1368, 437409), (24424, 3563, 165622, 226117, 268381, 281060), (306717, 437800, 498491, 454109, 45791, 427166), (440079, 197166, 514113, 24595, 172079, 106605), (529695, 239369, 361569, 565415, 72455, 244407)])
H_ = S*C.parity_check_matrix()*matrix(Permutations(n).random_element())

s = [sorted(random.sample([_ for _ in range(n)],t-1)) for i in range(len(secret))]
look_for_pankas = [H_*vector([random.randint(1,32) if j in s[i] else 0 for j in range(n)]) if secret[i] == '1' else vector([random.randint(1,p-1) for j in range(6)]) for i in range(len(secret))]


#v0id通过某些方法修改了自己的人体结构，看上去需要经历一些反混淆反编译才能重现世间。
secret = bin(bytes_to_long(v0id_part))[2:]

F = GF(2 ** 256, 'z')
z = F.gens()[0]
P = PolynomialRing(F, 'u, v')
u, v = P.gens()
PP.<x> = PolynomialRing(F)
x = PP.gens()[0]

h = u^2 + u
f = u^5 + u^3 + 1
on_curve = v^2 + h*v - f
h,f = h(u=x),f(u=x)

H = HyperellipticCurve(f, h)
J = H.jacobian()

def init():
    while 1:
        try:
            plain = random.randint(1,2^256)
            xx = F.fetch_int(plain)
            y, k = on_curve(u=xx, v=x).roots()[0]
            assert k == 1
            return - xx, y
        except:
            continue

look_for_v0id = [(3*J(H(init())))[0] if i == '1' else random.choice([(7*J(H(init())))[0],x^2+F.fetch_int(random.randint(1,2^256))*x+F.fetch_int(random.randint(1,2^256))]) for i in secret]

print(look_for_JBNRZ)
print(look_for_pankas)
print(look_for_v0id)

JBNRZ's part ———有待更新·标记 5/9

#JBNRZ开了修改器把自己卡在七教二楼阳台的墙壁中间。你就算知道他在哪，也没法摸到他。
secret = bin(bytes_to_long(JBNRZ_part))[2:]

q = 0x1a0111ea397fe69a4b1ba7b6434bacd764774b84f38512bf6730d2a0f6b0f6241eabfffeb153ffffb9feffffffffaaab
r = 0x73eda753299d7d483339d80809a1d80553bda402fffe5bfeffffffff00000001
k = GF(r)(q).multiplicative_order()
F = GF(q)
K2.<x> = PolynomialRing(F)
F2.<u> = F.extension(x^12+1)
E2 = EllipticCurve(F2, [0, 4+4*u])
o = E2.order()

P = E2.random_element()*(o//r)
Q = E2.random_element()*(o//r)
R = E2.random_element()*(o//r)
S = E2.random_element()*(o//r)

def random_gen_fg(P,Q,R,S):
    P,Q,R,S = random.randint(1,r-1)*P,random.randint(1,r-1)*Q,random.randint(1,r-1)*R,random.randint(1,r-1)*S
    f1 = (P._miller_(Q+S,r))
    f2 = (P._miller_(S,r))
    g1 = (Q._miller_(P+R,r))
    g2 = (Q._miller_(R,r))
    return P.weil_pairing(Q,r)+(f1/f2*g2/g1)

look_for_JBNRZ = [random_gen_fg(P,Q,R,S) if i == '1' else random.randint(1,q-1)*u+random.randint(1,q-1) for i in secret]

Pankas' part

#pankas用注释符把自己注释掉了，你必须使用一些过滤手段停止他的作弊行为。
secret = bytes_to_long(pankas_part)

p = 567811
F = GF(p)
n, k, r= 16, 10, 6
t = n//4

C = codes.GeneralizedReedSolomonCode([F(_+1) for _ in range(n)],k)
S = matrix(F,r,r,[(155790, 486108, 98452, 364639, 120720, 313488), (100323, 367952, 158314, 537951, 1368, 437409), (24424, 3563, 165622, 226117, 268381, 281060), (306717, 437800, 498491, 454109, 45791, 427166), (440079, 197166, 514113, 24595, 172079, 106605), (529695, 239369, 361569, 565415, 72455, 244407)])
H_ = S*C.parity_check_matrix()*matrix(Permutations(n).random_element())

s = [sorted(random.sample([_ for _ in range(n)],t-1)) for i in range(len(secret))]
look_for_pankas = [H_*vector([random.randint(1,32) if j in s[i] else 0 for j in range(n)]) if secret[i] == '1' else vector([random.randint(1,p-1) for j in range(6)]) for i in range(len(secret))]

犹记得当时出的时候特意卡了一些板子，但是具体过程已经说不上来了。调用的是Niederreiter system，隐私矩阵S和H已经完全给出，同时知道加密结果H_*v，权重在目标范围内，P矩阵只对解码结果的顺序有影响，因此此时整个加密系统在攻击者的眼中是透明的，可以使用伴随式解码直接进行攻击。

当然，题目里的error数值太小以至于可以用格子直接打出来，是一个大大大大非预期。

具体实现还是没忍住直接调了sageapi哈哈哈哈

from Crypto.Util.number import *
from sage.modular.overconvergent.hecke_series import ech_form
from sage.coding.decoder import Decoder, DecodingError
from sage.coding.grs_code import GeneralizedReedSolomonCode

class Syndrome_decode(Decoder):
    def __init__(self, code):
        super(Syndrome_decode, self).__init__(code, code.ambient_space(),
                "EvaluationVector")

    def _repr_(self):
        return "Key equation decoder for %s" % self.code()

    def _partial_xgcd(self, a, b, PolRing):
        prev_t = PolRing.zero()
        t = PolRing.one()

        prev_r = a
        r = b

        while(r.degree() >= t.degree()):
            q = prev_r.quo_rem(r)[0]
            prev_r, r = r, prev_r - q * r
            prev_t, t = t, prev_t - q * t

        return (r, t)
    
    def _forney_formula(self, error_evaluator, error_locator):
        C = self.code()
        alphas = C.evaluation_points()
        col_mults = C.parity_column_multipliers()
        ELPp = error_locator.derivative()
        F = C.base_ring()
        zero, one = F.zero(), F.one()
        e = []

        for i in range(C.length()):
            alpha_inv = one/alphas[i]
            if error_locator(alpha_inv) == zero:
                e.append(-alphas[i]/col_mults[i] * error_evaluator(alpha_inv)/ELPp(alpha_inv))
            else:
                e.append(zero)

        return vector(F, e)

    def decode(self,S):
        C = self.code()

        PolRing = C.base_field()['x']
        x = PolRing.gen()
        
        S = PolRing([i for i in S])

        a = x ** (C.minimum_distance() - 1)

        (EEP, ELP) = self._partial_xgcd(a, S, PolRing)

        e = self._forney_formula(EEP, ELP)
        return e

p = 567811
F = GF(p)
n, k, r= 16, 10, 6
t = n//4
data = 
C = codes.GeneralizedReedSolomonCode([F(_+1) for _ in range(n)],k)
S = 
H = C.parity_check_matrix()
D = Syndrome_decode(C)

flag = ''.join('1' if D.decode((matrix(F,i)*((S^(-1)).transpose()))[0]) else '0' for i in data)
print(long_to_bytes(int(flag,2)))

v0id's part——有待更新标记 5/9

#v0id通过某些方法修改了自己的人体结构，看上去需要经历一些反混淆反编译才能重现世间。
secret = bin(bytes_to_long(v0id_part))[2:]

F = GF(2 ** 256, 'z')
z = F.gens()[0]
P = PolynomialRing(F, 'u, v')
u, v = P.gens()
PP.<x> = PolynomialRing(F)
x = PP.gens()[0]

h = u^2 + u
f = u^5 + u^3 + 1
on_curve = v^2 + h*v - f
h,f = h(u=x),f(u=x)

H = HyperellipticCurve(f, h)
J = H.jacobian()

def init():
    while 1:
        try:
            plain = random.randint(1,2^256)
            xx = F.fetch_int(plain)
            y, k = on_curve(u=xx, v=x).roots()[0]
            assert k == 1
            return - xx, y
        except:
            continue

look_for_v0id = [(3*J(H(init())))[0] if i == '1' else random.choice([(7*J(H(init())))[0],x^2+F.fetch_int(random.randint(1,2^256))*x+F.fetch_int(random.randint(1,2^256))]) for i in secret]

串了超椭里相对常见的两个考点，也算是给自己好好复盘下。

前言